
| Spannweite | Leff = 10,00 m |
| Belastung | f = 0,1 kN/m |
| Querschnitt | b / h = 0,30 / 0,30 m |
| Biegesteifigkeit | EI = 0,5 kNm² |
| Dehnsteifigkeit | EA = 20 kN |

|
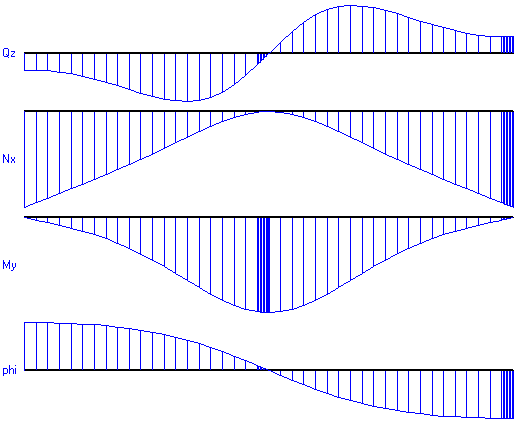
In nebenstehendem Bild sind die Verläufe von Querkraft, Normalkraft, Biegemoment und Verdrehung
dargestellt. Da die Zustandsgrößen konsequent auf die verformte Stabachse bezogen werden, ergibt
sich dieser Verlauf. Werden z.B. Querkraft und Normalkraft vektoriell addiert, erhält man den
nach Theorie 1. Ordnung berechneten Querkraftverlauf. Wie man weiterhin am Normalkraftverlauf erkennt,
wird durch die sehr große Verformung die Belastung jeweils an den Auflagern zum größten Teil
durch eine Normalkraft abgetragen. Die vertikalen Unterteilungen geben die benutzte Elementierung im Übertragungsverfahren an, der Benutzer braucht hingegen nur einen einzigen Stab zu modellieren. |
|
|
|
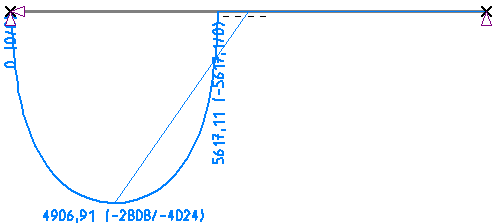
Die Verformung im nebenstehenden Bild ist ohne Überhöhung dargestellt (Einheit mm). Man sieht, wie sich
der Balken im Bereich der Auflager nahezu senkrecht nach unten verformt hat, so dass sich der hohe
Normalkraftanteil erklären lässt. Zu diesem Beispiel anzumerken sei, dass der Benutzer zwar nur einen Balken in seinem FE-Modell erzeugen muss. Eine gewisse Anpassung der Rechenparameter wie Abbruchkriterien für die Gleichgewichtsiteration oder maximale Segementgröße für das Übertragungsverfahren ist jedoch nötig, da eine gesicherte Konvergenz ansonsten nicht für alle möglichen Rechenparameter gegeben ist. |
 |
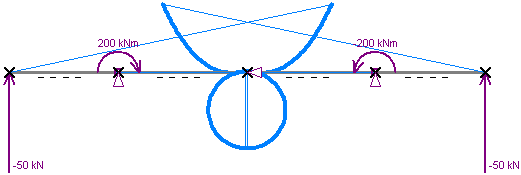
Mit ein wenig Geschick in der Wahl der Systeme und der Lastverläufe lässt sich damit so ziemlich jede in sich verschlungene Figur bewerkstelligen. Einige Verformungsverläufe der dem Programm beigelegten Beispieldateien sind im folgenden aufgeführt. Die Verformungen sind ohne Überhöhung dargestellt!
Geschichtlich interessant ist, dass sich bereits Leonard Euler mit der elastischen Linie
beschäftigte und die exakten Verformungsfiguren ohne (!) Computer berechnete. In der Tat
ist es mit dem Computer sehr schwierig, diesen meist labilen Gleichgewichts- oder
Verzweigungspunkten nahe zu kommen.
Ein interessantes Buch zu diesem Thema, auch wenn es schon ein wenig "älter" ist ;-)
Leonhardi Euleri Opera Omnia: The Rational Mechanics of flexible or elastic Bodies (1638 - 1788)

|

|
|---|---|
|